Geometrĭa III

Perspectiva

Unidad I

Conjunto de trazos que ayudan a representar en una superficie plana (como un papel o un lienzo) la tercera dimensión de objetos, dando sensación de profundidad y volumen. La perspectiva ayuda a recrear la profundidad y la posición relativa de los objetos comunes en un plano.

Elementos principales de la perspectiva:

*Líneas paralelas, van una al lado de la otra y, aunque sigan en un plano, nunca se encontrarán.
*Líneas oblicuas, son líneas que parten de puntos distintos una al lado de la otra, pero que en su recorrido se encontrarán en algún punto.
*Líneas convergentes, partes de dos partes distintas para luego encontrarse en un punto.
*Líneas divergentes, parten de un mismo punto a distintas direcciones.

Con la inplementación de estos tipos de líneas podrás lograr efectos interesantes.

Características principales de la perspectiva:
1-Super posicion de formas.
2-Convergencia de lineas paralelas.
3-Disminucion de tamaño.
4-Escorzo.

Los 7 elementos de la perspectiva visual:

 1- Punto de Vista (PV): Da la posición y orientación del observador, el efecto pictórico obtenido en una perspectiva viene determinado por la posición del punto de vista y eñ ángulo visual.


 
2- Centro de Vista o punto principal (c): En la proyección ortogonal el PV (ojo del observador) sobre el plano de cuadro,

3- Cono Visual: Es el ángulo de visión máximo dentro del cual lo que se ve no queda deformado (45- 60 grados) cualquier cosa que se quiera dibujar en perspectiva tiene que entrar dentro de este cono visual, ya que de lo contrario quedaría muy distorcionado.

4- Línea de Horizonte (LH): Es una recta horizontal perteneciente al plano de cuadro (perpendicular a la visual del observador) y siytuada a la misma altura que el ojo del observador (PV) en consecuencia el punto principal pertenece siempre a la línea de horizonte.

5- Línea de Tierra (LT): Es la intersección del plano geometral con el plano del cuadrado, se usa como base para tomar medidas.


6- Plano del cuadro (PC): Es el plano trscendente perpendicular a la línea visual del observador, a través del cual el observador mira lo que ve en perspectiva.


7- Punto de fuga (PF): Todos los conjuntos de rectas paralelas convergen en un punto de fuga común en la perspectiva.
 

Tipos de perspectiva:

Perspectiva a un punto de fuga (perspectiva lineal) 

La perspectiva a un punto de fuga tiene efecto cuando un conjunto principal de rectas paralelas es paralelo al plano (perpendicular a la vista del observador) las rectas verticales (eje z) y horizontales (eje x) pertenecientes a estos planos permanecen verticales y horizontales mientras que en el otro conjunto principalde rectas horizontales al ser perpendiculares al plano de cuadro, fugan las líneas de horizonte en un punto.Sirven para representar los espacios interiores, esenas de calles y disposiciones axiales. Son relativamente fáciles de construir pero a veces resultan mdemasiado deslucidas o estáticas. 
  

Perspectiva a dos puntos de Fuga: 
La perspectiva a dos puntos de fuga conserva la verticalidad de las rectas verticales, pero los dos conjuntos de rectas horizontales (eje x-y) son oblicuos al plano de cuadro y cada conjunto tiene su propio punto de fuga.

La perspectiva a dos puntos de fuga es la más utilizada. Al revés que la perspectiva a un punto de fuga no tiene que ser simétríca ni estática, ya que presenta una vista más natural para el observador. Se puede utilzar para espacios y formas tanto interiores como exteriores y es adaptable a la mayoría de las situaciones.

Perspectiva a tres puntos de fuga:
Tiene los tres conjuntos principales de rectas (eje x-y-z) oblicuos al plano de cuadro y en consecuencia tiene tres puntos de fuga principales.

 1.1.3 Proyecciones Ortogonales (proyeccción diédrica)

Tienen su origen en el siglo XVIII entre los años 1746-1818, cuando su inventor el matemático francés Gaspar Monge, considerado el padre de la Geometría Descriptiva Moderna, logró normalizar algunos procesos gráficos, denominandolos Sistema de Monge, el cual consiste en descomponer un objeto tridimensional, llevándolo a producidos gráficos bidimensionales representados en un plano.

El término proyección se refiere a la representación gráfica de un objeto o una figura colocados perpendicularmente sobre el plano. Todos los objetos arquitectónicos son básicamente, volúmenes, es decir, objetos desarrollados en tres dimensiones “Tridimensionales” (ancho X, alto Y; profundidad Z). 

La palabra ortogonal se deriva de dos palabras de origen Griego:

ORTHOS: Que significa recto, correcto o en ángulo recto.
GRAPHICOS: Que significa describir con líneas de dibujo

Se denomina proyección ortogonal al sistema de representación que nos permite dibujar en diferentes planos  un objeto situado en el espacio.

 Proyección Diédrica: Este sistema consiste en una proyección ortogonal en la que se utilizan dos planos de proyección uno horizontal (PH) y uno vertical (PV), los cuales al interceptarse en un ángulo recto (90º) forman un ángulo diedro recto. La intercepción de dos planos que se cortan recibe el nombre de Arista, la cual es común ambas proyecciones o sea la intercepción recibe el nombre de Línea de Tierra (LT).

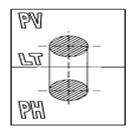
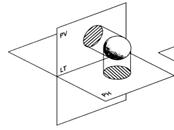
 Distribución de Vistas Según la Norma ISO.
Se denominan vistas principales de un objeto, a las proyecciones ortogonales del mismo sobre 6 planos, dispuestos en forma de cubo.

Si situamos un observador según las seis direcciones indicadas por las flechas, obtendríamos las seis vistas posibles de un objeto.

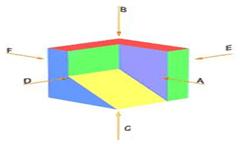
Las vistas reciben los siguientes nombres:
1.- Vista A = Vista Principal o Alzado.
2.- Vista B = Vista Superior o Planta.
3.- Vista C = Vista Inferior.
4.- Vista D = Vista Lateral Izquierda.
5.- Vista E = Vista Lateral Derecha.
6.- Vista F = Vista Posterior.




Hay tres planos principales de proyección: horizontal, vertical y de perfil (ancho X, alto Y; profundidad Z). . Estos planos se intersecan uno a otro en ángulo recto formando el primero, segundo, tercero y cuarto cuadrante. Técnicamente se puede proyectar un objeto en cualquiera de estos cuadrantes.

Para la disposición de las diferentes vistas sobre el papel, se pueden utilizar dos variantes de proyección ortogonal de la misma importancia:

- El método de proyección del primer diedro, también denominado Europeo
- El método de proyección del tercer diedro, también denominado Americano

En ambos métodos, el objeto se supone dispuesto dentro de un cubo, sobre cuyas seis caras, se realizarán las correspondientes proyecciones ortogonales del mismo.

La diferencia esta en que, mientras en el sistema Europeo, el objeto se encuentra entre el observador y el plano de proyección, en el sistema Americano, es el plano de proyección el que se encuentra entre el observador y el objeto.

Una vez realizadas las seis proyecciones ortogonales sobre las caras del cubo, y manteniendo fija la cara de la proyección del alzado (A), se procede a obtener el desarrollo del cubo, que como puede apreciarse en las figuras, es diferente según el sistema utilizado.



El desarrollo del cubo de proyección, nos proporciona sobre un único plano de dibujo, las seis vistas principales de un objeto, en sus posiciones relativas. Con el objeto de identificar, en que sistema se ha representado el objeto, se debe añadir el símbolo que se puede apreciar en las figuras, y que representa el alzado y vista lateral izquierda, de un cono truncado, en cada uno de los sistemas.

La proyección de primer cuadrante se usa principalmente en Europa. En EE.UU., como es el caso del sistema ASA (American Standard Asociation), hacen más práctica la proyección de tercer cuadrante, esto debido a que cuando las vistas de un objeto proyectado en el tercer cuadrante se abaten sobre el plano vertical, todas las vistas aparecen en su posición natural.

En esta unidad trabajaremos en el sistema americano ASA; esto no significa que le restemos importancia al sistema europeo DIN (Deutche Industric Normen), la razón estriba en que la gran mayoría de textos de dibujo técnico que encontramos en nuestro medio, manejan el sistema americano, no obstante el sistema europeo se ha venido trabajando ampliamente en nuestro país.

Cuando se desea indicar el método de proyección, se debe colocar, en la esquina inferior derecha del dibujo, el símbolo de proyección ISO (International Standards Organization)

 

1.1.4. Proyecciones Axonométricas

El sistema axonométrico se desarrollo para suplir las desventajas del sistema diédrico, es decir, poder visualizar un elemento mecánico de una forma rápida y sin conocimientos previos. 

Este sistema se subdivide en dos principales, el sistema axonométrico ortogonal y el sistema axonométrico oblicuo. La diferencia entre ambos es la dirección de los rayos de proyección respecto del plano en el que se proyectan, la cual será perpendicular o con otro ángulo en cualquiera de ambos casos.

SISTEMA AXONOMÉTRICO ORTOGONAL
Se divide en tres subsistemas :

* Isométrico: El más utilizado por su comodidad. Los tres ejes forman los mismos ángulos.

* Dimétrico: Dos de los ángulos entre ejes son iguales.
* Trimétrico: Los tres ángulos son distintos.

SISTEMA AXONOMÉTRICO OBLICUO
Tiene muchas variantes, y algunas de las más conocidas son :
* Perspectiva caballera: Muy cómoda para trabajar en verdadera magnitud con una de las caras
* Perspectiva Militar: Aquella en la que la planta es la que está en verdadera magnitud
* En esta solo se aprecia dos de las tres caras de un cubo

La perspectiva axonométrica se utiliza mucho para realizar los diseños previos. Es una representación neutral, las líneas del objeto quedan paralelas y acercan el abjeto hacia el espectador. Para obtener la primero se realiza a mano alzada lo que se quiere, para ver si se puede realmente desarrollar la pieza, el espacio, el lugar u objeto que se va a proyectar. Los interioristas utilizan bastante esta modalidad para dar dibujos con medidas exactas a los industriales como carpinteros, herreros y todos los oficios de una obra.

Los ejes deben realizarse con escuadra y cartabón. Marcaremos una línea vertical, llamada eje Z y posteriormente dos líneas con un ángulo de 120º. Para realizar esta medida utilizaremos el cartabón por el vértice más estrecho, que es el de 30º. Así nos quedara el ángulo antes mencionado. Una vez realizados los ejes de coordenadas solo nos quedará ir dibujando la pieza con las medidas dadas. 

Todo el dibujo se debe realizar paralelo a los ejes principales.                                                                                                                                        

Perspectiva Caballera (X,Y,Z)

La perspectiva caballera Teniendo los ejes principales X, Y, Z (figura a la izquierda) utilizaremos una reducción para una buena representación espacial. La escala que debemos reducir solo será en el eje Y, aplicando la mitad de la dimensión del objeto que hay que dibujar. Es utilizada cuando una pieza, por su complejidad, no es fácil de interpretar a través de sus vistas como, por ejemplo, la de los manuales de instrucciones de todo tipo de maquinaria. 

Perspectiva cónica

La perspectiva cónica es la más compleja de representar gráficamente, pero la más utilizada en arquitectura y decoración para representar grandes edificios y volúmenes. Ésta es la que más se aproxima a la visión real, equivale a la imagen que observamos al mirar un objeto con un solo ojo.

La vemos muchas veces en carteles de complejos y edificaciones inmobiliarias que están en construcción. Es el resultado de cómo va a quedar la nueva obra, zona edificada, ajardinada y piscina. De esta manera los compradores pueden tener una idea de lo que van a adquirir.

 

Geometría I

Introducción a la Geoemtría

UNIDAD I

La Geometría: Es una rama de las matemáticas que tiene que ver con los problemas métricos, de ahí el origen de la palabra (geo= tierra; metría= medida). Abraham Wald, matemático rumano, hizo importantes contribuciones a la geometría.

La Geometría permite el cálculo del área y diámetro de figuras planas de su  superficie y el volumen de cuerpos sólidos. La aplicación particular de los conocimientos geométricos ha generado el tratamiento de otras esferas: surge así la geometría analítica, la topología, etc.

  
En la actualidad ya no cabe hablar de geometría en el antiguo sentido de una rama autónoma de la matemática, sino más bien de un "lenguaje geométrico", aplicado a un grupo de propiedades integrantes de una matemática unificada y unificadora. Según la naturaleza de esas propiedades se tienen distintas geometrías, que con sus caracteres generales son:

Geometría analítica: Es más un método que una geometría, pues consiste en el estudio de las figuras con recursos algebraicos, mediante la introducción de coordenadas que en general establecen una correspondencia entre los entes geométricos: puntos, curvas, superficies y los números y ecuaciones.

Geometría diferencial: En cierto sentido es una aplicación de la anterior, ya que consiste en estudiar las propiedades de las curvas y de las superficies con los recursos del análisis infinitesimal.

Geometría euclidiana: Se basa en los postulados de los Elementos de Euclides y en ella es válida la propiedad de que por un punto puede trazarse una sola paralela a una recta.

Geometría no euclidiana: En ésta no vale el postulado de la paralela única, por tanto admite que por un punto pueden trazarse dos paralelas a una recta (Geometría hiperbólica) o ninguna paralela (Geometría elíptica); así tenemos también la Geometría de dimensiones, descriptiva, métrica, afine y proyectiva, la topología, etcétera.

1.1 OBJETO DE ESTUDIO DE LA GEOEMTRIA

 La geometría elemental se divide en dos partes, geometría plana (estudia la figuras planas, que tienen únicamente dos dimensiones: largo y ancho) y geometría del espacio (estudia las propiedades de los cuerpos geométricos provistos de largo, ancho y altura o profundidad). 

¿QUÉ ESTUDIA LA GEOMETRÍA?
La geometría es el estudio de los conocimientos espaciales de las formas que hace la mente humana para su comprensión en un esquema de representación en base a planos bidimensionales (figuras geométricas), tridimensionales (cuerpos geométricos).

¿DÓNDE SE APLICA LA GEOMETRÍA? 

Tiene su aplicación práctica en física, mecánica, cartografía,  astronomía,  náutica,  topografía, balística, arquitectura, escultura, dibujo, etc. 

1.2 Historia de la Geometría

Los conocimientos geométricos de los babilonios: Hacia el año 2200 a.C. aplicaron reglas para calcular áreas de rectángulos, triángulos isósceles, trapezoides y círculos. En la medición de los sólidos, daban soluciones relacionadas con paralelepípedos, cilindros y prismas rectos, que aplicaban a trabajos de excavación de canales para riego. Conocieron también que el ángulo inscrito en un semicírculo es recto, que los lados homólogos de triángulos semejantes son proporcionales, de la relación entre los lados de un triángulo rectángulo y la relación entre la longitud de una circunferencia y su diámetro, tomando en valor de 3 para p .

            En el siglo VI a.C. el matemático Pitágoras colocó la piedra angular de la geometría cinetífica al demostrar que las diversas leyes arbitrarias e inconexas de la geometría empírica se pueden deducir como onclusiones lógicas de un número limitado de axiomas o postulados. Estos postulados fueron considerados por Pitágoras y sus discípulos como verdades evidentes; sin embargo, en el pensamiento matemático moderno se consideran como un conjunto de supuestos útiles pero arbitrarios.

            Aunque existen intentos anteriores, la primera sistematización de ese conjunto de conocimientos cristaliza en los elementos de Euclides (300 a.C.), que si bien no comprendían todos los conocimientos matemáticos de la época, su estructura es tan sólida y orgánica que aun hoy constituye la base de los textos de geometría elemental. 

            Apolonio de Perga estudió la familia de curvas conocidas como cónicas y descubrió muchas de sus propiedades fundamentales. Las cónicas son importantes en muchos campos de las ciencias físicas; por ejemplo, las órbitas de los planetas alrededor del sol son fundamentalmente cónicas.

            Arquímedes, uno de los grandes científicos griegos, hizo un considerable número de aportaciones a la geometría. Inventó formas de medir el área de ciertas figuras curvas así como la superficie y el volumen de sólidos limitados por superficies curvas, como paraboloides y cilindros. También elaboró un método para calcular una aproximación del valor pi, la proporción entre el diámetro y la circunferencia de un círculo y estableció que este número estaba entre 3 10/70 y 3 10/71.

            Así, con Euclides, Arquímedes y Apolonio, la geometría griega llega a su culminación. La geometría avanzó muy poco desde el final de la era griega hasta la Edad Media. 

El siguiente paso importante en esta ciencia lo dio el filósofo y matemático René Descartes, cuyo tratado El Discurso del Método, publicado en 1637, hizo época. Este trabajo fraguó una conexión entre la geometría y el álgebra al demostrar cómo aplicar los métodos de una disciplina en la otra. Éste es un fundamento de la geometría analítica, en la que las figuras se representan mediante expresiones algebraicas, sujeto subyacente en la mayor parte de la geometría moderna.

            Otro desarrollo importante del siglo XVII fue la investigación de las propiedades de las figuras geométricas que no varían cuando las figuras son proyectadas de un plano a otro.

            La geometría sufrió un cambio radical de dirección en el siglo XIX. Los matemáticos Carl Friedrich Gauss, Nikolái Lobachevski y János Bolyai, trabajando por separado, desarrollaron sistemas coherentes de geometría no euclidiana. Estos sistemas aparecieron a partir de los trabajos sobre el llamado "postulado paralelo" de Euclides, al proponer alternativas que generan modelos extraños y no intuitivos de espacio, aunque sí coherentes.

           

Geometría planaLa geometría plana estudia las fi…guras planas, que tienen únicamente dos dimensiones: largo y ancho.

Para comprender la geometría plana de manera mas clara, es indispensable, comenzar por la de…finición de conceptos elementales hasta llegar a nociones más complejas. 
                 

1.3. Conceptos básicos de geometría

Para el estudio de la geometría, es indispensable conocer el concepto intuitivo de punto, recta y plano. Estos son términos no definidos que proveen el inicio de la geometría.
                 
 El punto: Un punto señala una posición en el espacio. Conceptualmente carece de longitud, anchura y profundidad.



La línea: La prolongación de un punto se convierte en una línea. Desde el punto de vista conceptual, la línea tiene longitud, pero carece de anchura y profundidad.

Ejemplo Linea Recta

Línea recta: Una línea recta es la trayectoria mínima entre dos puntos situados en el espacio. La recta puede presentarse de tres formas en un plano: de punta, como una recta en verdadera magnitud, como una recta acortada.

Ejemplo Linea Paralela

Lineas Paralelas: Dos rectas son paralelas cuando equidistan en toda su longitud.








Lineas Perpendiculares: Dos rectas son perpendiculares cuando se cortan formando un ángulo de 90 grados.

Ejemplo Linea Perpendiculares

Lineas Secantes: Dos rectas son secantes si tienen un punto en comun.

Semirecta: Una semirrecta es una porción de recta, que tiene principio pero no final. 

Concepto del Segmento:





Plano: La geometria basica opera sobre un plano. 

1.4.  Instrumentos

Caja de compaces. Incluye un compás con complementos de lápiz y tiralíneas, un compás divisor, un compás de círculos, una tachuela de centrado.

Aguja cortadora. Se emplea en lugar de la mina de lápiz, para recortar círculos de papel o lámina.

Compás cortador. Con tornillo moleteado, que no se desajusta fácilmente, incluso con cortados repetidos.

Tiralíneas con bisagra cruzada. Para el trazado de líneas con la regla con cualquier color diluido, la bisagra cruzada facilita el limpiado. Para el trazado de líneas con la plantilla de curvas y para cualquier color diluido es apropiado el tiralíneas curvo.

Tablero de dibujo. De plástico con guía por ranura Rundum para la regla T, óptimo para dibujo técnico, montaje de letras, etc.

Tablero con bastidor de inclinación. Recomendable para trabajos con color, puesto que la posición oblicua provoca el efecto de un caballete y resulta más fácil hacerse con una visión de conjunto del trabajo que en una mesa horizontal.

Regla T. Según se prefiera, disponible en plástico, plexiglás, aluminio o acero, con o sin división milimétrica.

Escuadras y transportadores. Pueden emplearse de todos los tamaños para el trabajo con la regla T.

Reglas. Deben ser de plexiglás o un material similar, tener división milimétrica y una longitud entre los 30 y los 50 cm.

Regla de corte. Para cortar papeles y cartones. Las hay de acero o aluminio con suplemento de acero a lo largo del cual se produce el corte. En la parte inferior se recomienda un apoyo de goma, con el objeto de que la regla no se desplace al cortar.

Plantillas de curvas. Las hay con las más diversas curvas, hipérbolas, parábolas, elipses, etc., y pueden utilizarse como auxiliares del dibujo.

Plantillas de circunferencias y elipses. Son auxiliares del dibujo, y también pueden utilizarse en las operaciones de pulverizado, siempre que se cubran adecuadamente.

Escobilla de dibujo. Para retirar los restos de goma de borrar del bosquejo y de la mesa.

Difumino. Rollito de papel con punta en ambos extremos para el esfuminado del lapicero, carbón, pastel.

Materiales

Lápices. Los más comunes se encuentran clasificados en el comercio mediante números o 
letras y son los siguientes:
6B, 5B: lápices muy blandos de ennegrecimiento intenso, para el boceteado y el sombreado.
4B, 3B: lápices blandos para el bocetado.
2B, B, HB, F: lápices semiblandos para el bocetado y dibujado.
H, 2H, 3H, 4H, 5H: lápices duros y muy duros para el marcado, el dibujado y el calco.
6H, 7H, 8H: lápices extremadamente duros, apropiados únicamente en aplicaciones especiales como cartografía, litografía, etcétera.
Lápices sin madera formados por una barrita de grafito de unos 8 mm de diámetro recubierto de laca, y muy indicados para esbozos y dibujos.
Lápices marcadores de mina fina.

Gomas de borrar. También se han acreditado el borrador de plástico Staedtler Mars y el Rotring para láminas y papel.

Plumas de dibujo. Para dibujos en tinta china negra o de color. Puntas desde finas a extrafinas.

Tinta negra. En tintero, tinta china negra para pluma y pincel.

Tinta china de dibujo negra. En tintero, botella o cartucho para pluma y pincel, se puede diluir con agua destilada.

FW-Pen-Opake. En tintero, tinta china blanca, cubriente, en tintero con instilador, para pluma, Isograph a partir de 0,5 mm, y pincel; práctica para trabajos de cubrimiento.

Lápices de colores de madera. Marcas: Stabilio, Castell-Color, Prismalo de Caran d´Ache; todos acuarelables en agua.

Minas de colores para lápices portaminas. Marcas: Castell-TK-Color, en 17 colores acuarelables en agua. Koh-i-noor-Color, en 24 colores, acuarelables en agua, pero sólo se ajustan a un portaminas especial porque las minas son más gruesas.

Tiza grasa. Como la de pastel, de base grasa y amplio surtido de colores, no debe fijarse. Marcas: Jaxon; Neocolor 1 de Caran d´Ache.

Lápices de fieltro. Los hay con tinta china soluble en agua, tinta china de alcohol (no soluble en agua) y tinta china luminosa. Los lápices de fieltro son sólo parcialmente resistentes a la luz.

Papeles de trazado y de rotulador. En paquetes de DIN A4, A3, A2; papel semitransparente para trabajos de boceto y de lápiz de fieltro, que no embebe la tinta.

Papel transparente. Para el bocetado, el más adecuado es un rollo de 33 cm (24 g/m2 y 45 g/m2).

Papeles de dibujo. En hojas y rollos, de 150 a 300 g/m2, con las superficies suaves y ásperas.

Cartones de dibujo. En planchas de 0,4-3,2 mm de espesor. Las superficies se consideran superlisas, lisas, ásperas y extraásperas; las dos últimas, muy indicadas para acuarelar.

Cartón de montaje. Para pautas (layouts) y montajes de letras, espesor 1,5 mm.

Lámina reticular. En hojas, autoadhesiva, en parte también transferible, muchas estructuras como retículas lineales, de puntos, tramas degradadas, etc.

Papel de grafito. Se utiliza en el calcado, las líneas calcadas pueden borrarse.

Papel de greda. Se emplea para el calcado sobre fondos oscuros, las líneas también pueden borrarse.